 A news item by the BBC has led many viewers to my blog in recent days. According to a recent report, primary teachers in Great Britain are scared of math, which results in poor math teaching.
A news item by the BBC has led many viewers to my blog in recent days. According to a recent report, primary teachers in Great Britain are scared of math, which results in poor math teaching.
I can’t say much about primary teachers, especially in Great Britain, but in 2006 I consulted with about 100 teachers of adult numeracy, GED and Adult Basic Education math classes (whole numbers through algebra) about bringing their teaching practices into line with research findings. I didn’t find them scared of math, but I did find specific barriers that prevented them from improving their teaching practice. (You will find a fuller description of my study in the introduction to Changing the Way We Teach Math.)
As a basis for discussion with these math instructors, I used principles from “Instructional Strategies for Teaching Adult Numeracy Skills” by Lynda Ginsburg and Iddo Gal. They include strategies such as determining what learners know before beginning instruction on a topic; looking at learners’ attitudes about math; using manipulatives; developing skills in estimation and mental math; group work; providing opportunities for learners to talk about math; and using real life math problems to promote the transfer of math learning.
Everyone knows what the “best practices” are
Almost without exception, the instructors I talked with were familiar with all of those strategies, and generally agreed that they would be effective, yet by and large THEY DID NOT USE THEM.
Instructors want to change their practice
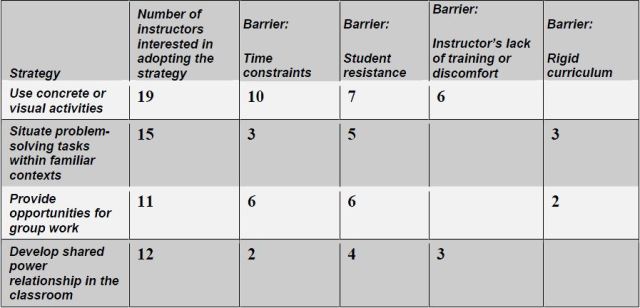
When I asked the 100 instructors which of the strategies they didn’t currently use, but would like to adopt, two of the top four choices were content oriented: Instructors were interested in using concrete and visual activities, and in using real life contexts for problem solving. The other two of the top four choices were about process: providing opportunities for group work, and developing a shared power relationship with students.
What gets in the way?
I asked them what barriers they faced in implementing the strategies that they said they would like to use. As expected, they said that time constraints (cited by 21 instructors) and a rigid curriculum (5) got in their way. Grant Wiggins has an interesting post about dealing with these issues.
Even more instructors, however, cited process barriers in implementing their chosen strategies: student resistance (22) and the instructor’s lack of training, or discomfort (9).
No one mentioned instructor resistance to changing their practice, but I suspect that “time constraints” and “rigid curriculum” mask some instructor resistance to dealing with student resistance, emotions, and the drama of group work.
What makes these strategies difficult to implement?
Many (dare I say most?) math classes in literacy, ABE and GED programs are still taught in the old-fashioned way, with power centered in the teacher, and the text and the test governing the content and method.
In order to understand why instructors find it difficult to change the way they teach, let’s take a closer look at the strategies promoted as best practices.
- Many of them ask both teachers and students to step out of their usual roles, and change is always difficult.
- Some of them ask teachers to make themselves vulnerable, and to deal with emotions, their own and their students’.
- Some of them ask teachers to rely on their students’ knowledge of things the teacher does not and possibly cannot know.
- Some of them ask students to be open about their lack of knowledge and skills, lacks they have been hiding for years.
- Some of them are in conflict with the needs and assumptions of administration and funding bodies, which want to count completions and register grades.
A need for revolutionary thinking
I think that we have to name the problems of implementation more clearly before we can adopt these strategies, before we can change our practice to bring it into line with research and theory.
In naming and describing the barriers to implementation, however, we must be revolutionaries in our approach, for a revolution in practice is necessary. We must be willing to look at the factors that make instructors resistant to change. We must be willing to look at why instructors and administrators are unwilling to have the messiness of real numeracy learning come into their classrooms.
Finally, we must be willing to work with students to find out what invitations to participate need to be sent, how bridges can be built, what it will take for students to believe that we are willing to change, and that the change will be beneficial.
A scary prospect indeed.
Related articles
- Kate Nonesuch. Math Strategies in Context
- Kate Nonesuch. Changing the Way We Teach Math
- Kate Nonesuch. More Complicated Than It Seems
- Grant Wiggins. A simple move to avoid coverage and make time for more learning


Pingback: Math Strategies in Context | Working in Adult Literacy
Many people from South Africa reading this post this week. I encourage you to click on the links at the bottom of the post for more details.
Explain in detail how you teach ABET level 1 learners Fractions
Thanks for your question. I took the opportunity you gave me to write a new post, and to attach a specific guide to teaching fractions. You’ll find it here: Math Strategies in Context.
you can use a sliced bread to teach fractions
Thanks for this idea, Sontaga. How do you use the bread? Do you get students to divide it up, or do you divide it and show them? Or some other way? I’ve never used a slice of bread to teach fractions, but I can see how it would work. Has anyone else used bread like this? How did it go?
EXPLAIN HOW YOU WOULD TEACH YOUR LEARNERS PLACE VALUE.
Thanks to you as well–your comment made me do some thinking, and the result was this blogpost, along with a pdf of specific ideas for teaching place value. Math Strategies in Context.
Just found your blog… Great! Thanks…
why do you think abet practitioners are afraid to teach numeracy?
Thanks for your question, Precious. A couple of times a year there are many people from South Africa who find this blog by googling the question “Why are ABET teachers afraid to teach math.” You are the first to leave a comment, which I appreciate very much. I’m curious about why so many people are looking for the answer to that question. Are you all taking a class? What are your ideas about why so many ABET (Adult Basic Education and Training) teachers are afraid of teaching math?
Anyway, I can think of some possible answers.
In my part of the world, most people who teach students at the very basic level are more experienced in teaching reading, writing–basic literacy. They often do not have much experience teaching numeracy, and often haven’t done any math since they left school themselves.
Many such instructors can “do” math, but don’t really understand what’s behind many of the procedures they have to teach. For example, they know that you “invert and multiply” to divide by a fraction, but they can’t explain what division means, or why that procedure gets the right answer. And we are all usually nervous and afraid to stand up in front of a class when we are not sure of ourselves.
And here in Canada, most adult students have spent years in school, struggling with math, and still don’t know it. So the students generally don’t like math, or are afraid of it, or “know” they can’t do it. So teachers have to come up with some new ways of approaching math, because the old ways didn’t work for those students.
Teachers have to change their ways of teaching. Students have to deal with new, unfamiliar ways. Both have to deal with their own resistance and they are all swimming in a sea of emotions. No wonder many are afraid to jump in!
Looking forward to hearing from you about your experience!
The list of factors you describe is very interesting. I certainly recognize them in my own career as a teacher.
Once, toward the end of my career, I taught an algebra class – a subject I’m not particularly comfortable with. I stuck rigidly to the book and a schedule and counted on being positive, enthusiastic, caring, etc to accomplish their ability to do the math. Ever since I’ve been ashamed of my work in that class.Lots of students passed and I daresay learned some algebra – a good number always learn in spite of us teachers. When I imagine doing the kind of math teaching you advocate, I quail. I wasn’t certain I knew the math well enough to chance a free wheeling exploration. I was too tired to dance through honest confrontation with what they didn’t understand. And I knew from years of experience that my caring/respecting/believing attitude would bring the best effort out of the students. So they did their best, but I didn’t.
When I think back, I think the key was – I was too tired. Our careers as teachers seldom include the breaks and supports needed to keep up the effort it takes to be a revolutionary teacher. Just one more thing to add to the list of why we don’t do the best we know.
Thanks for the post.
Thanks for your honesty, Evelyn. You remind me of a tennis champion–Even when her best game is off, she finds a way to win.